Instantaneous field of influence
Definition
In this section we will discuss the basic geometric concepts necessary for achieving sensor fusion.
A sensor is an electromechanical device that translates the energy of a physical phenomenon into a signal. The objective of sensor fusion is to determine that the data from two or more sensors correspond to the same phenomenon. We say that the data of two or more sensors correspond to the same phenomenon if the energy of the signal originates from the same place and time. Location and time are of the primary importance, so we will begin with describing how the sensor data corresponds to location and time.
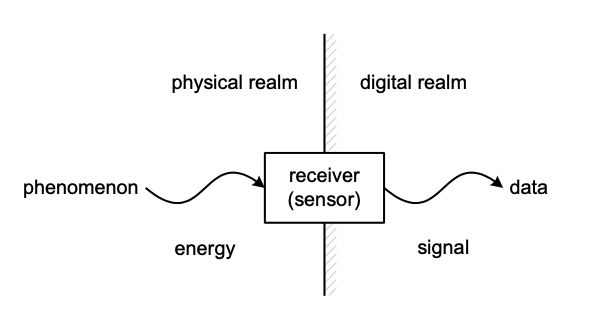
Figure 12 Sensor reference model
A sensor data element is the smallest possible group of bits from a signal that can be equated with a phenomenon. An example of a sensor data element would be the red value of a pixel in a digital camera.
The signal of sensor data will equate to energy from a finite volume of space at a finite period of time. We call that finite volume of space at a finite period of time the instantaneous field of influence (IFOI). To achieve sensor fusion, we must define the instantaneous field of influence for the sensor data.
It has been common in the sensor community to differentiate remote sensors from in situ sensors. Remote sensors are considered to measure phenomena occurring at a distance while in situ sensors measure phenomena occurring at the location of the sensor. Cameras and radar are considered remote sensors while thermometers and microphones are considered in situ sensors.
The sensor reference model shown in Figure 12 implies that a sensor responds to energy received at a particular point and time from a particular instantaneous field of influence. From the perspective of sensor fusion, all sensors are in situ sensors.
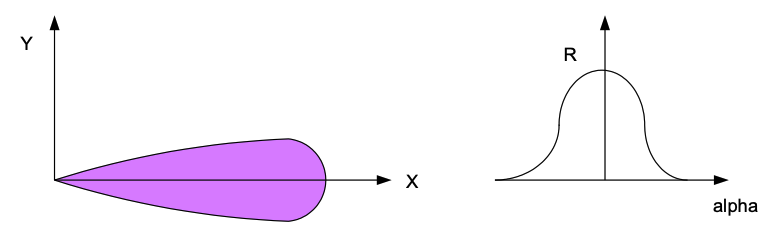
Figure 13 Typical shape of an IFOI plotted in Cartesian and polar coordinates
The shape of an IFOI can be defined as a range at a given angle for a given constant energy response. The energy is always a dimensionless ratio. One would define the IFOI for 0.5 power ratio, which is -3 dB. This ratio is the typical power curve that engineers expect. For complex sensors, it may be necessary to define multiple IFOI shapes for varying power ratios. An IFOI is typically a polar shape in Cartesian coordinate system and a continuous function in the spherical coordinate system, as shown in Figure 13. In two dimensions, we would provide range rho for angle alpha. In three dimensions, we would provide range rho for angles alpha and beta.
Camera example
To explain IFOI, we will walk through the simple example of a small digital camera. The camera has 640 by 480 pixels. We must determine the look angle by experiment to determine alpha, the angle in the X-Y plane, and beta, the angle in the X-Z plane, as shown in Figure 14.
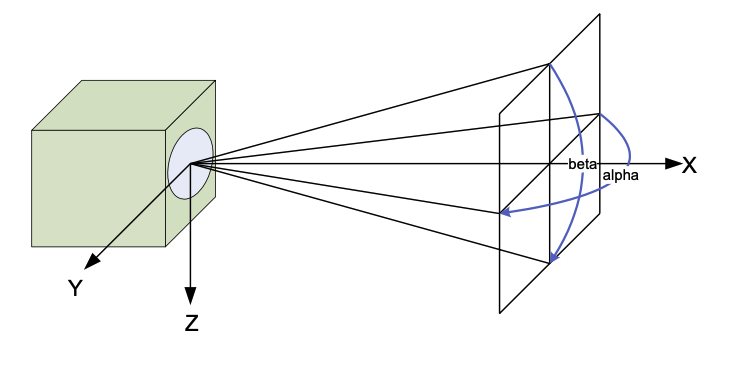
Figure 14 Look angle of a simple camera
As a simple means to calculate the look angle, we would measure how wide and tall the camera can see at different distances from the camera and take an average of the values.
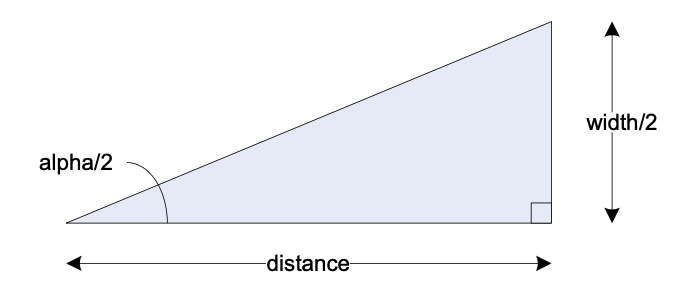
Figure 15 Look angle calculation
In our example, the alpha angle is 0.667 radians and the beta angle is 0.520 radians.
Each data element has an IFOI. Within our camera, the red, green and blue values of a pixel all have the same IFOI. We must determine the dimensions of the curve shown in Figure 13 for a pixel. The alpha and beta dimensions of the curve are easy enough. Assuming linear distribution, alpha angle for a pixel would be 0.667 divided by 640, or 0.00104 radians, or from -0.00052 to 0.00052, to be more accurate. The beta angle is solved similarly.
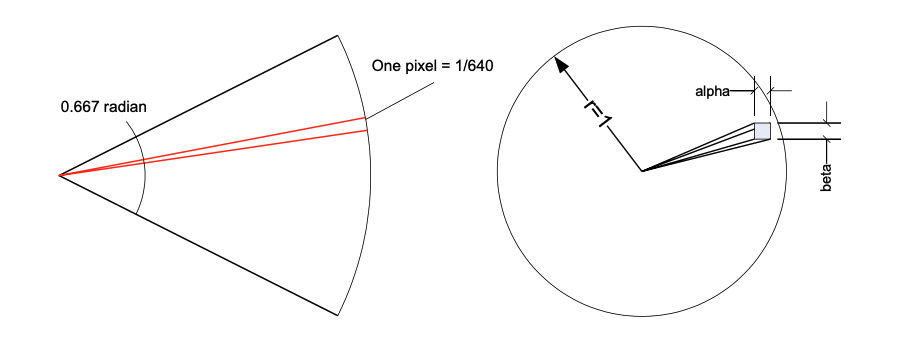
Figure 16 IFOI of one pixel is a fraction of a sphere
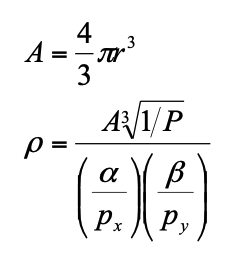
The rho value of the IFOI shape is not so straightforward. In the above equation, A represents the area on the surface of a sphere. P is the power ratio, which is always less than one. As stated earlier, alpha is the field of view in the X-Y plane and beta is the field of view in the X-Z plane. The values px and py are the number of pixels in the respective direction. For our camera, there are 640 by 480 pixels. The alpha is 0.667 radians and the beta is 0.520 radians. We want the 0.5 power ratio, which is -3 dB, a standard engineering point. If we map to a radius of 1, then the value of rho is as follows:
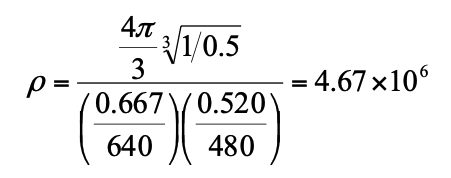
As one might expect, the IFOI of the pixel is very narrow and very long. The alpha angle is - 0.00052 to 0.00052 at 4.67x10^6, as shown in Figure 17. It is so narrow and long that it could be treated as a ray. With other sensors, the shape of the IFOI is not so obvious and exceedingly important.
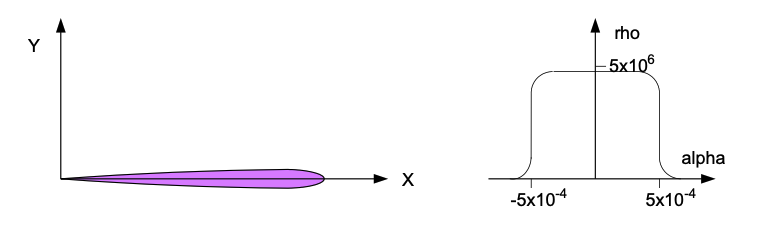
Figure 17 Example pixel IFOI
We have defined the shape of the IFOI for each pixel in our example, but we are missing a very critical component to complete the model. Each pixel or, more accurately, each IFOI needs a coordinate reference frame.